기본-변형-확장 예제로 공학도의 자신감을 길러주는 미분·적분 입문서!
책소개
미분적분이 두려운 이여,
이제 자신감을 갖고 당당히 마주하자!
공학을 전공하는 학생에게는 반드시 넘어야 할 산이 있다.
바로 듣기만 해도 머리가 지끈거리는 미분과 적분이다.
미분과 적분을 공부하는 데에는 천재적인 머리가 필요하지는 않다.
단지, 어떤 공식을 어떻게 활용하는지 제대로 알지 못했고,
다양한 유형의 문제를 해결해보는 연습을 충분히 하지 못했을 뿐이다.
이 두 가지만 충족된다면, 미분과 적분은 더 이상 두려움의 대상이 아니다.
이 책은 이런 두려움을 극복할 수 있도록
유형에 따라 공식을 활용하는 방법을 보여주고,
충분한 연습을 할 수 있게 도와준다.
【이 책의 특징】
저자소개
목차
Chapter 01 | 집합과 함수
1.1 집합 / 연습문제
1.2 함수 / 연습문제
1.3 지수함수와 로그함수 / 연습문제
1.4 삼각함수 / 연습문제
1.5 역함수와 역삼각함수 / 연습문제
Chapter 02 | 함수의 극한과 연속
2.1 함수의 극한 / 연습문제
2.2 함수의 극한 계산 / 연습문제
2.3 연속함수 / 연습문제
Chapter 03 | 미분 Ⅰ
3.1 미분의 정의 / 연습문제
3.2 미분의 기본 정리 / 연습문제
3.3 합성함수의 미분법 / 연습문제
3.4 음함수와 매개변수함수의 미분법 / 연습문제
Chapter 04 | 미분 Ⅱ
4.1 삼각함수의 미분법 / 연습문제
4.2 로그함수와 지수함수의 미분법 / 연습문제
4.3 쌍곡선함수의 미분법 / 연습문제
4.4 고계 도함수 / 연습문제
Chapter 05 | 미분의 활용
5.1 1계 도함수의 활용 / 연습문제
5.2 평균값 정리 / 연습문제
5.3 로피탈의 법칙 / 연습문제
5.4 2계 도함수의 활용 / 연습문제
5.5 극댓값과 극솟값의 활용 / 연습문제
Chapter 06 | 부정적분
6.1 부정적분의 정의와 기본 정리 / 연습문제
6.2 치환적분법과 부분적분법 / 연습문제
6.3 삼각함수의 적분법 / 연습문제
6.4 부분분수 적분법 / 연습문제
Chapter 07 정적분
7.1 정적분의 정의와 기본 정리 / 연습문제
7.2 미분적분학의 기본 정리 / 연습문제
7.3 이상적분 / 연습문제
Chapter 08 | 정적분의 활용
8.1 영역의 넓이 / 연습문제
8.2 입체도형의 부피 / 연습문제
8.3 호의 길이 / 연습문제
Chapter 09 | 극좌표와 곡률
9.1 극좌표 / 연습문제
9.2 극좌표함수의 그래프 / 연습문제
9.3 곡률 / 연습문제
Chapter 10 | 벡터
10.1 벡터의 정의 / 연습문제
10.2 벡터의 내적 / 연습문제
10.3 벡터의 외적 / 연습문제
찾아보기
출판사리뷰
【누구를 위한 책인가】
이공계열의 학생들이 전공을 학습하는 과정에서 자주 접하게 되는 미분적분의 기본 이론과 계산 방법을 설명하는 책으로, 고등학교에서 배운 수학 지식을 바탕으로 쉽게 계산 능력을 향상시킬 수 있도록 구성했다. 부족한 부분을 스스로 보완할 수 있도록 자세한 예제 풀이와 단계별로 연습문제를 제시하여 미분적분 계산 능력을 향상시키고자 하는 학생들에게 도움이 될 것이다.
【무엇을 다루는가】
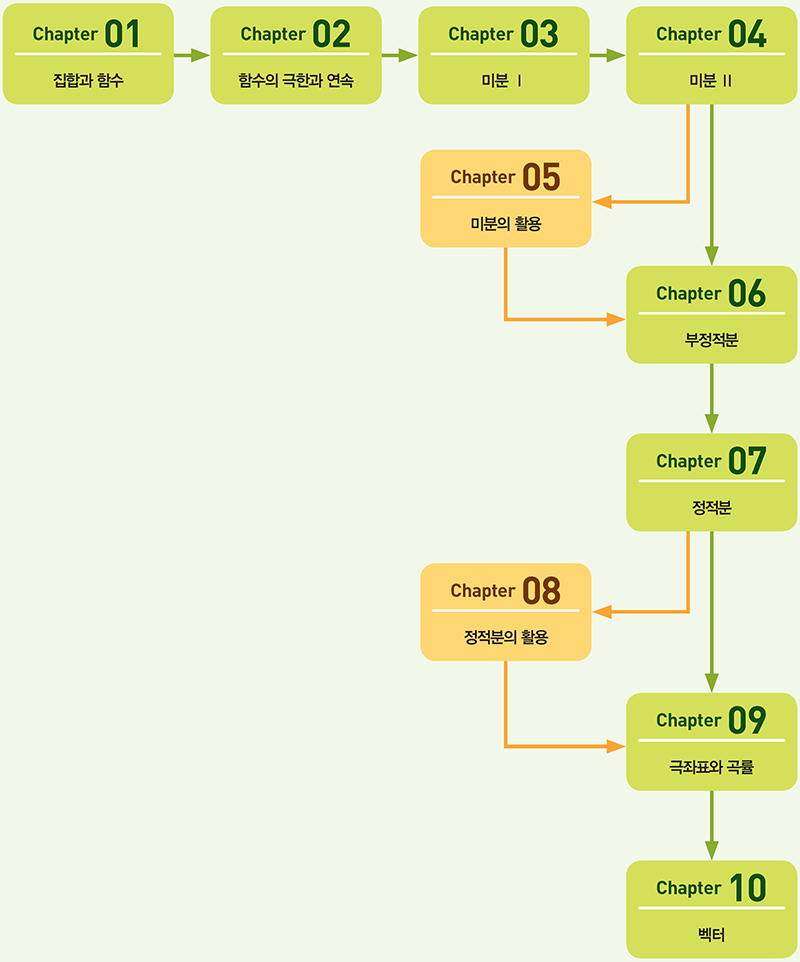
【부/장별 내용 요약】
➊ 집합과 함수(1장)
수학의 가장 기본이 되는 집합을 정의하고, 집합들 사이의 관계를 설명하는 함수에 대해 소개한다.
➋ 함수의 극한과 연속(2장)
극한의 존재를 확인하는 방법, 극한과 연속의 관계를 알아보고, 중간값 정리를 활용할 수 있는 방안에 대해 설명한다.
➌ 미분(3장~5장)
미분의 정의, 다양한 함수의 미분법을 체계적으로 익힐 수 있는 방법을 알아보고, 미분을 활용하여 다양한 문제를 푸는 방법을 설명한다.
❹ 적분(6장~8장)
적분의 정의, 정적분의 계산법을 익힌 후, 이를 활용하는 방법을 설명한다.
❺ 극좌표와 곡률(9장)
직교좌표와 전혀 다른 개념의 극좌표를 도입하고, 이를 이용하여 곡선의 휜 정도를 나타내는 방법을 설명한다.
❻ 벡터(10장)
공학 문제에 자주 활용되는 3차원 벡터공간을 설명하고, 내적과 외적의 의미와 계산법에 대해 설명한다.
추천도서
오탈자 등록
공개용 답안
